Introduction to Graphs
A graph is a mathematical structure that consists of nodes, also known as vertices, and edges, which connect pairs of nodes. These components represent relationships between objects, where nodes can symbolize entities and edges depict the connections or interactions between them. Graphs are fundamental in various fields, including computer science, network theory, and social sciences, for modeling and analyzing complex systems and relationships.

Types of Graph
- Empty Graph: A graph is considered an empty graph if it has no edges, meaning it consists solely of isolated vertices (nodes) with no connections between them.
- Trivial Graph: A graph consisting of just one node is referred to as a trivial graph.
- Simple Graph: A graph is considered simple if it contains no loops. These types of graphs are unique.
- Multigraph: These graphs include loops and may have multiple edges.
Line Set
A line set in graph theory refers to a collection of edges within a graph. This set can be used to represent various structures or properties of the graph, such as cycles, paths, or cuts. Linesets are essential for analyzing the connectivity and other topological features of graphs. They can also be used in algorithms that involve edge operations, such as finding minimum spanning trees or detecting cycles.
| Node | Actor | Lives Near | | ---- | ------- | --------------------- | | n₁ | Allison | Ross, Sarah | | n₂ | Drew | Eliot | | n₃ | Eliot | Drew | | n₄ | Keith | Ross, Sarah | | n₅ | Ross | Allison, Keith, Sarah | | n₆ | Sarah | Allison, Keith, Ross |
Lines
| Lines | Connection | | ----- | ---------- | | l₁ | (n₁, n₅) | | l₂ | (n₁, n₆) | | l₃ | (n₂, n₃) | | l₄ | (n₄, n₅) | | l₅ | (n₄, n₆) | | l₆ | (n₅, n₆) | For instance, consider the following line set (set of edges): $l_2(n_1, n_6)$, $l_6(n_5, n_6)$, $l_1(n_1, n_5)$. This represents a sub graph within the main graph that is also complete. This serves as an example of a line set.
In some contexts, a lineset might specifically denote the set of all edges in a graph, but it can also refer to a subset of edges that satisfy certain conditions or criteria relevant to a particular problem or analysis.
Sub-graphs : Graph Within A Graph ??

A subgraph is a smaller graph that is derived from a larger graph by selecting a subset of its vertices and edges. It retains the structure and relationships of the chosen elements within the original graph, allowing for focused analysis or manipulation of specific parts of the data. Subgraphs are useful for examining particular aspects of a network without the complexity of the entire structure.
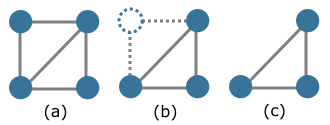
Here, in the image above, we observe the original graph in (a). We then remove the top-left node from the graph. Since we've deleted a node, we must also remove the edges connected to it, as edges are associated with two nodes, which can be the same or different. Therefore, by deleting a node, we must also delete its edges, resulting in the graph shown in (c).
Formal Definition for Completeness
![[Pasted image 20250327232704.png]]
Let $G = (V, E)$ represent a graph, where $V$ denotes the set of vertices and $E$ denotes the set of edges.
A graph $H = (V', E')$ is defined as a subgraph of $G$ if the following conditions are met:
- $V' \subseteq V$, implying that every vertex in $H$ is also present in $G$.
- $E' \subseteq E$, implying that every edge in $H$ is also present in $G$.
- For every edge $e \in E'$, its incident vertices are also in $V'$. That is, if an edge belongs to $H$, then the vertices it connects must also belong to $H$.
Dyads
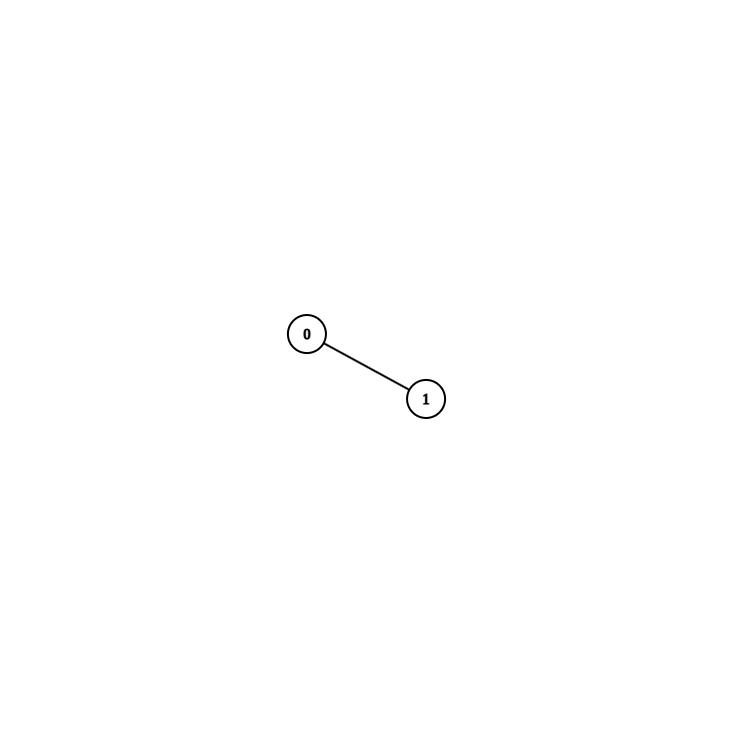
In graph theory, a dyad refers to a pair of vertices that are connected by an edge. Dyads are fundamental units in the study of graph structures and their properties.
In sociology, a dyad serves as a foundational element, representing the smallest possible social network. The term "dyad" originates from the Ancient Greek word δυάς (duás), meaning 'pair'.
Triads
A triad in graph theory generally refers to three nodes with at least two edges among them—either forming an open triad (like A–B and B–C but A–C missing) or a closed triad (a triangle).
he study of triads is crucial for understanding the local structure of a graph. Triads can be classified based on the presence or absence of edges between the vertices, such as open triads (one edge) and closed triads (three edges forming a triangle). Analyzing triads helps in identifying patterns and properties within complex networks.
![[Pasted image 20250327234257.png]]
Open Triads
Open triads consist of three individuals where only two pairs are directly connected. This structure allows for potential new connections to form.
In an open triad, individuals A and B are friends, as are B and C, but A and C are not yet connected. An example of this is when you have a friend who introduces you to another friend, creating a connection between you, your friend, and their friend. This is what we refer to as an open triad.
Closed Triads
Closed triads involve three individuals where all pairs are directly connected, forming a complete network of relationships.
This configuration features robust, mutual connections between all three individuals. For instance, consider a trio of close friends; each member shares a strong bond with the others, resulting in a closed triad.
Open Triad to Closed Triad Transition in Social Networks

In sociology, the concept of triad closure refers to the process where an open triad transitions into a closed triad. This occurs when individuals A and C, who were not previously connected, form a friendship due to the existing friendship between A and B, and B and C. This new connection between A and C completes the triad, transforming it into a closed structure with mutual ties among all three individuals.
Nodal Degrees

In network analysis, nodal degrees refer to the number of connections or edges emanating from a specific node. This metric is crucial for understanding a node's centrality and influence within the network. Higher nodal degrees often indicate more significant roles or greater connectivity for the node in question.
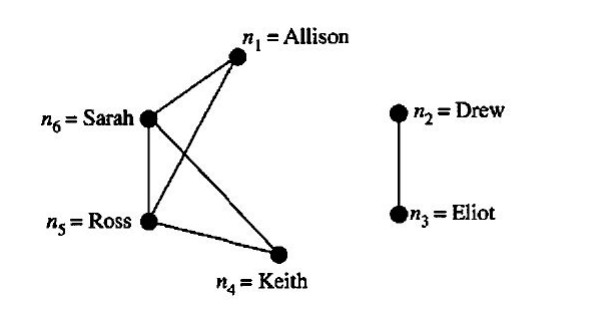
- Allison: Nodal degree of 2
- Drew: Nodal degree of 1
- Eliot: Nodal degree of 1
- Keith: Nodal degree of 2
- Ross: Nodal degree of 3
- Sarah: Nodal degree of 3
Types of Graph
Connected Graph A connected graph is one where you can navigate from any node to any other node. For instance, in a social network, consider a group of friends where everyone knows each other directly or through mutual friends. If you can send a message from any person to any other person in the group, either directly or through intermediaries, the social network forms a connected graph.
Complete Graph A complete graph is one where every node is connected to every other node, meaning all nodes have the same degree. In a social network context, imagine a small team where each member is directly connected to every other member. If everyone in the team follows each other on a social media platform, this forms a complete graph, as each node (team member) has the same number of connections (follows every other member).
Disconnected Graph A disconnected graph is one where there are nodes or groups of nodes that cannot be reached from certain other nodes. In a social network, consider two separate friend groups that do not know each other. If there is no mutual friend or connection between the two groups, the social network is a disconnected graph. For example, if Group A and Group B have no common members or indirect connections, they form separate components within the graph, making it disconnected.
Geodesic Distance

A geodesic is a term that refers to the shortest path between two points on a curved surface. The word itself comes from the Greek words "geo," meaning "earth," and "daiein," meaning "to divide." In essence, a geodesic is the most direct route on a given surface, such as the surface of a sphere or any other curved space.
The geodesic distance is always defined between a pair of vertices. Therefore, the next time you want to ask for directions from Bengaluru to Chennai, you should ask:
"Hello, kind person. May I know the geodesic distance between Bengaluru and Chennai, assuming all roads are modelled as edges and major cities are modeled vertices as graphs?"
Given this, how do you think it will be applicable in the context of graph theory and social networks?
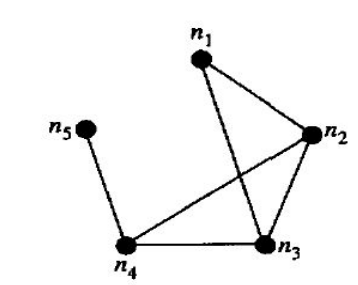
In this graph, the geodesic distance between n1 and n2 is 1, as it only requires traversing 1 edge. Now, consider the path from n1 to n3. There is a route through n1 -> n2 -> n3, but the geodesic distance does not account for this because it is not the shortest. The shortest distance is actually n1 -> n3 via the direct edge.
Bipartite Graph
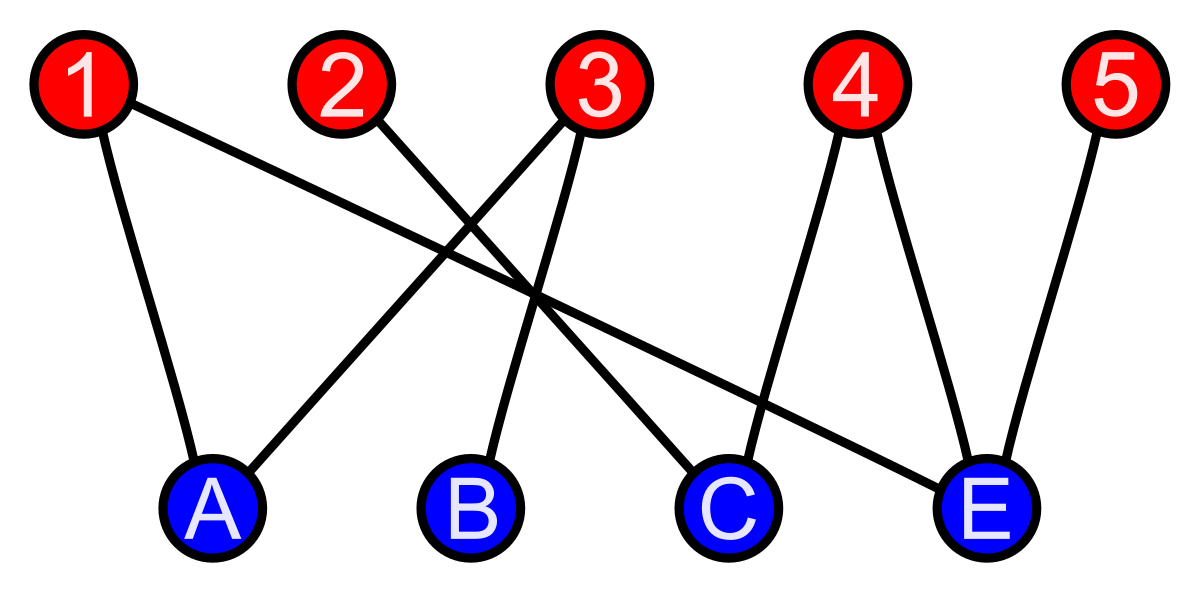
A bipartite graph is a type of graph whose vertices can be divided into two disjoint sets such that no two graph vertices within the same set are adjacent. This structure ensures that every edge connects a vertex in one set to a vertex in the other set, making it useful in various applications like matching problems and network design.
Complete Bipartite Graph

A complete bipartite graph is a special type of bipartite graph where every vertex in one set is connected to every vertex in the other set. This structure ensures that there are no edges between vertices within the same set, and every possible edge between the two sets is present. It is denoted as where $m$ and $n$ represent the number of vertices in each set.
Eccentricity of a Node in a Graph
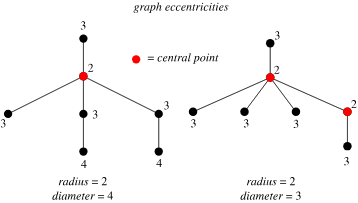
Meaning of Eccentricity
The term "eccentricity" in graph theory refers to the maximum distance between a vertex and any other vertex in the graph, and it is named so because it measures how "off-center" or distant a vertex is from others.
Formal Definition
For a vertex $v$ in a graph $G$, the eccentricity $e(v)$ is defined as:
$$e(v) = \max(d(v, u))$$
where $d(v, u)$ is the shortest path distance between $v$ and any other vertex $u$ in the graph.
Eccentricity Calculation
The eccentricity of a node ( v ) is determined by finding the distance from ( v ) to every other node ( u ) in the graph. These distances are stored in an array, and the maximum value in this array is identified as the eccentricity.
Here is a basic Python code snippet to illustrate this process
def calculate_eccentricity(graph, node):
"""
Calculate the eccentricity of a given node in a graph.
Parameters:
graph (dict): A dictionary representing the graph. Keys are nodes, and values are lists of neighboring nodes.
node (any): The node for which to calculate the eccentricity.
Returns:
int: The eccentricity of the node.
"""
def distance(source, dest):
"""
Abstracted distance function to calculate the distance between two nodes.
Parameters:
source (any): The source node.
dest (any): The destination node.
Returns:
int: The distance between the source and destination nodes.
"""
# Implement the distance calculation here
pass
max_distance = 0
for dest in graph:
if dest != node:
dist = distance(node, dest)
if dist > max_distance:
max_distance = dist
return max_distance